Todavía me sorprende encontrar en la universidad alumnos que piensan que la economía “es cosa de letras”, cuando la tendencia es lo opuesto.
No sólo en términos académicos donde cualquier publicación (tesis, “paper” científico…) debe tener una consistente base numérica que refrende las hipótesis; si no también en términos reales donde encontramos numerosos ingenieros y gente de ciencias puras que dan el salto a las empresas y demuestran su poderío gracias a un amplio conocimiento, estudio y entendimiento de los números.
Por ello en economía, en finanzas, no podemos obviar el poder de los datos y debemos aprender no sólo a redactarlos, si no a explicarlos, refrendarlos y proyectarlos.
La parte numérica en la economía toma como base la contabilidad y la estadística para (principalmente) con la econometría y las matemáticas financieras dar solución a los problemas.
¿Para qué sirven las matemáticas financieras?
Podemos decir que son una rama de las matemáticas aplicadas que tiene como objetivo el análisis, proyección y valoración de conceptos relativos a los mercados financieros, teniendo como objetivo base la valoración económica del dinero en diferentes momentos de tiempo.
Así, por ejemplo, nos permiten entre otras cosas:
- Proyectar una cantidad económica hacia el futuro o hacia el pasado para conocer su equivalencia en dos momentos dispares de tiempo.
- Calcular los tipos de interés o de rentabilidad de préstamos o proyectos.
- Estudiar y elaborar cuadros de amortización de créditos.
- Conocer el riesgo de un proyecto.
El conocimiento del valor real del dinero en dos momentos de tiempo (principal objetivo de estas matemáticas) se basa en la idea de equivalencia de capitales en dos instantes distintos en base a un tipo de interés, coste de oportunidad o tasa que normalmente se denomina como “i”.
Dos acciones principales en las matemáticas financieras
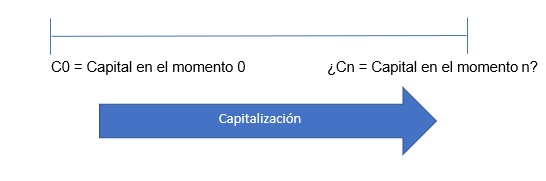
Capitalización
Consiste en la traslación de la cantidad de dinero actual hacia el futuro en base a una cuota de interés.
Esto lo podemos representar de la siguiente manera:
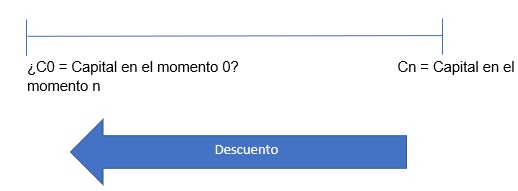
Descuento
Consiste en la traslación de la cantidad de dinero actual hacia el pasado en base a una cuota de interés.
Otra cosa que tenemos que tener en cuenta es el tipo de proyecto en el que estamos, es decir, si este cuenta con un interés simple o compuesto.
Decimos que un proyecto de interés simple es aquel en el que cada año obtenemos una rentabilidad y esta es retirada del proyecto; un proyecto de interés compuesto es aquel donde dejamos en dicho proyecto el interés, de tal manera que obtenemos más dinero que en el caso simple ya que los intereses siguen generando intereses.
De esta manera, obtenemos las primeras y principales fórmulas de las matemáticas financieras:
Pongamos un ejemplo, imaginémonos que queremos saber a cuánto dinero equivalen 2.000 Euros hoy en 3 años, teniendo en cuenta un interés del 5%.
Un ejemplo de descuento sería saber a cuánto dinero equivale hoy 2.000 Euros de dentro de 3 años, teniendo en cuenta un interés del 5%.
Este pequeño texto es sólo una píldora de lo que se puede llegar a hacer con estas matemáticas, desde saber cuanto dinero tenemos que poner cada mes para poder contar en el momento de nuestra jubilación de X euros; para conocer las cuotas a abonar en una hipoteca a 30 años por el valor de una casa; poder comparar préstamos en base a un tipo de interés…


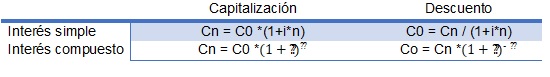






Muchas Gracias Licenciado. Estoy tomando notas de su informe para realizar mi trabajo del tecnologico , y me gusta la manera franca y sencilla en la explica.